Railsを4.2.7.1にアップデートをしてrspecを実行すると、以下のエラーが発生するようになった。

1
2
3
4
5
6
7
8
9
10

$ bundle exec rspec spec
[DEPRECATION] `last_comment` is deprecated.  Please use `last_description` instead.
[DEPRECATION] `last_comment` is deprecated.  Please use `last_description` instead.
[DEPRECATION] `last_comment` is deprecated.  Please use `last_description` instead.
[DEPRECATION] `last_comment` is deprecated.  Please use `last_description` instead.
[DEPRECATION] `last_comment` is deprecated.  Please use `last_description` instead.
......................................................................................................

Finished in 2.33 seconds (files took 8.78 seconds to load)
102 examples, 0 failures

grepしてみたところ、rspecで使用していた。

1
2
3

$ hw last_comment vendor/bundle
vendor/bundle/ruby/2.2.0/gems/rspec-core-3.2.2/lib/rspec/core/rake_task.rb
84:        desc "Run RSpec code examples" unless ::Rake.application.last_comment

rspecをアップデートしたら出なくなった。

1
2
3
4
5
6
7

$ bundle update rspec-rails

$ bundle exec rspec spec
......................................................................................................

Finished in 2.33 seconds (files took 8.85 seconds to load)
102 examples, 0 failures

iPhone6の画面が真っ暗になり操作できなくなった。
画面は真っ暗だが、Siriが反応するので電源は入っている模様。

電源ケーブルを挿してみたが症状は変わらず。
電源ボタンを押しても反応がない。

修理となるとショップまで足を運ぶのが面倒くさいし、色々とクリアしないといけない問題が浮かんでくる。
まずは、家から出るのが1つめの難関だ。
高い確率で上の子がついてくるとダダをこね、下の子は泣くだろう。それを見た妻からは怪訝な顔をされる。
なんとか家を出れたとしても、近くのショップの駐車場が空いていないかもしれないし、駐車できたとしても待ち時間があるかもしれない。以前、近くのドコモショップにいったら1時間くらい待ち時間がかかりますと言われたことがある。
また、ショップ店員に見せても要領の得ない回答をされて、無駄に時間がかかってしまう可能性もありそうだ。
そういうことを考えるとショップに行くのがとても億劫になる。

自分でなんとかできないだろうかと自宅のPCでググった。そして、iPhoneを強制再起動する方法を見つけた。
やりかたは、電源ボタンとホームボタンを10秒以上長押しする。
するとアップルのリンゴマークが表示されるので、そのまま待っていると再起動する。
見事、このやり方で復活した。

iPhoneが操作不能になった場合、以下のことを試してみるとよい。

• 電源ボタンで電源を切って再起動
• 電源コードを挿す
• 強制再起動する
• どうしようもないのでショップに相談する

私のチームではCIで自動的にLINTをする仕組みを構築しています。
この仕組みにより、レガシーコードでテストコードがない環境でもシンタックスエラーの混入を防ぐことができます。

中身はシンプルで以下のスクリプトを作成して、CIプラットホームで実行するようにします。

php-lint.sh

1
2
3
4
5
6
7
8

#!/bin/sh

RESULT=`find . -type f -name "*.php" -exec php -l {} \; 2>&1 | grep "PHP Parse error"`

if [ "$RESULT" != "" ];then
    echo "$RESULT"
    exit 1
fi

例えば、Droneでチェックする場合は以下のように設定します。

.drone.yml

1
2

script:
  - ./php-lint.sh

Docker HubとGitHubを使ってDockerイメージの自動ビルドを行う方法を紹介します。

自動ビルドのメリット

自動ビルドのメリットは以下です。

• 常に最新のイメージがDocker Hubに用意される
• Dockerfileが公開され使う人が安心できる
• READMEも常に最新のものがDocker Hubに公開される

Docker Hubを利用するには事前にアカウントの作成が必要です。
Docker Hubのアカウントの作成は以下を参考にしてください。

• Create a Docker Hub account & repository

Docker Hubで自動ビルドの設定をする

すでにDockerfileがGitHubで管理されていることを前提に話しを進めます。

Docker Hubにログインしたら「Profile > Settings > Linked Accounts & Services.」を選択します。

GitHubを使うのでGitHubのパネルを選択し、認証をしてください。
認証が成功すると、以下のような画面になります。

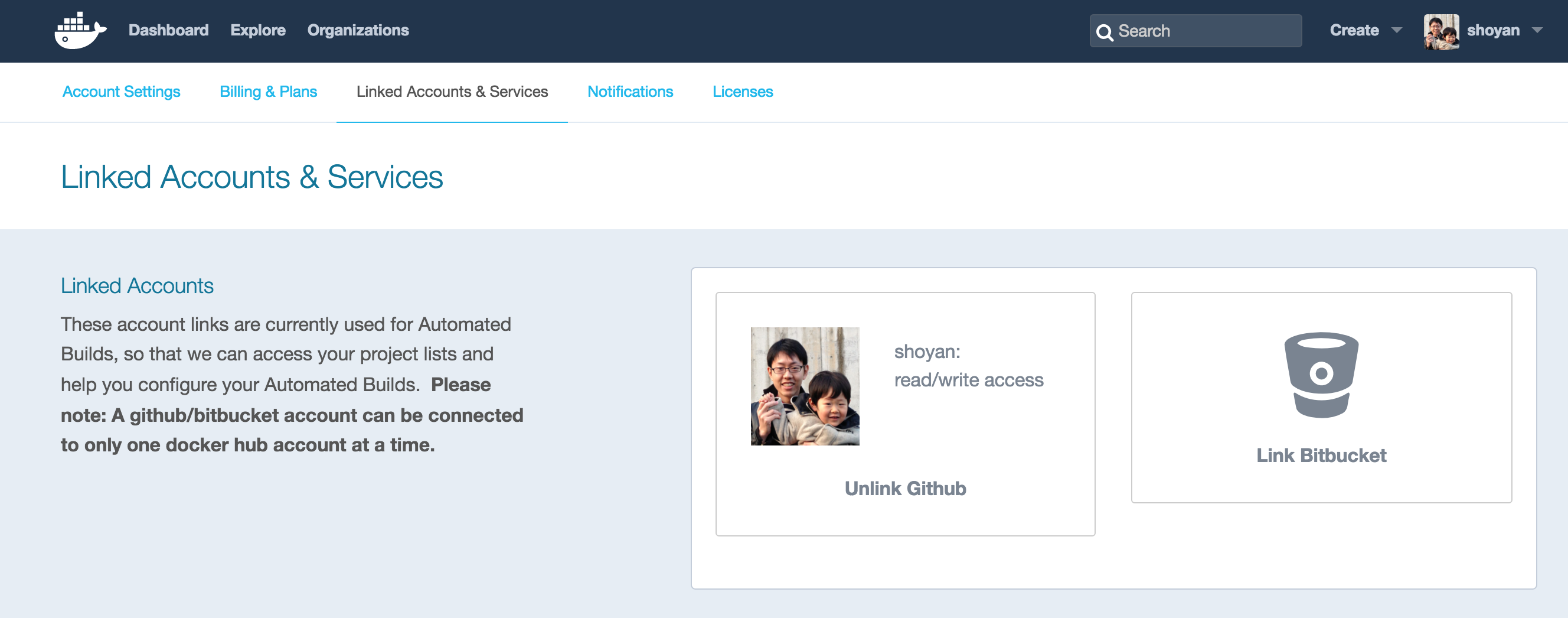
認証が済んだら、Docker Hubにリポジトリを作成します。

「 Create > Create Automated Build」を選択します。

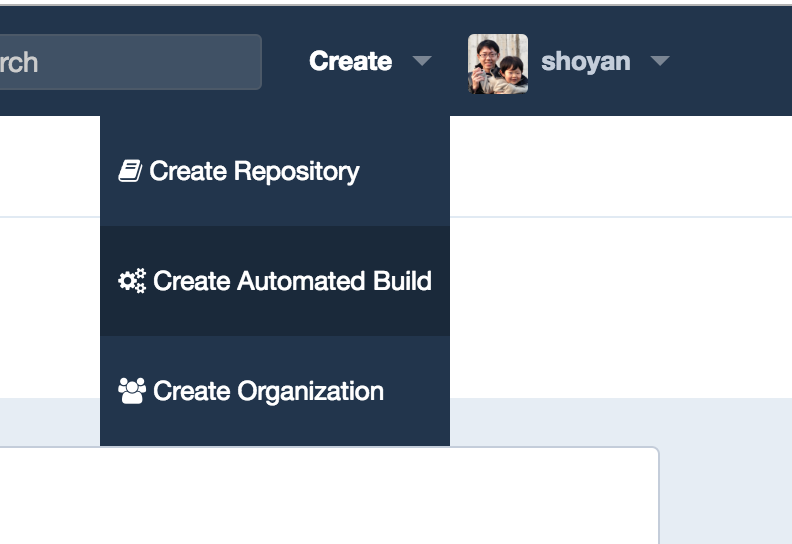
すると以下の画面が表示されます。

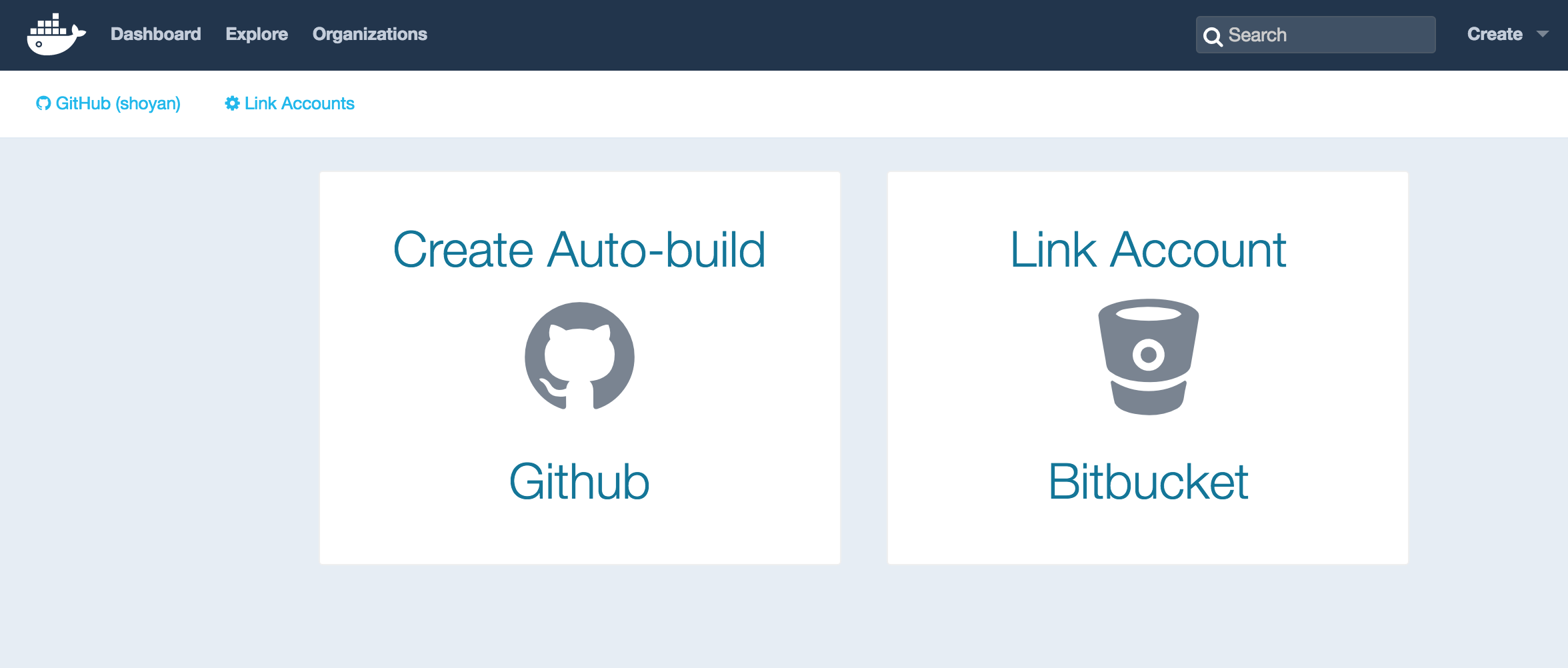
GitHubを選択すると 「Users/Organizations」とリポジトリを選択できる画面になるので、自動ビルドを行うリポジトリを選択します。

Createボタンを押すと登録され、Docker Hubに表示されるようになります。

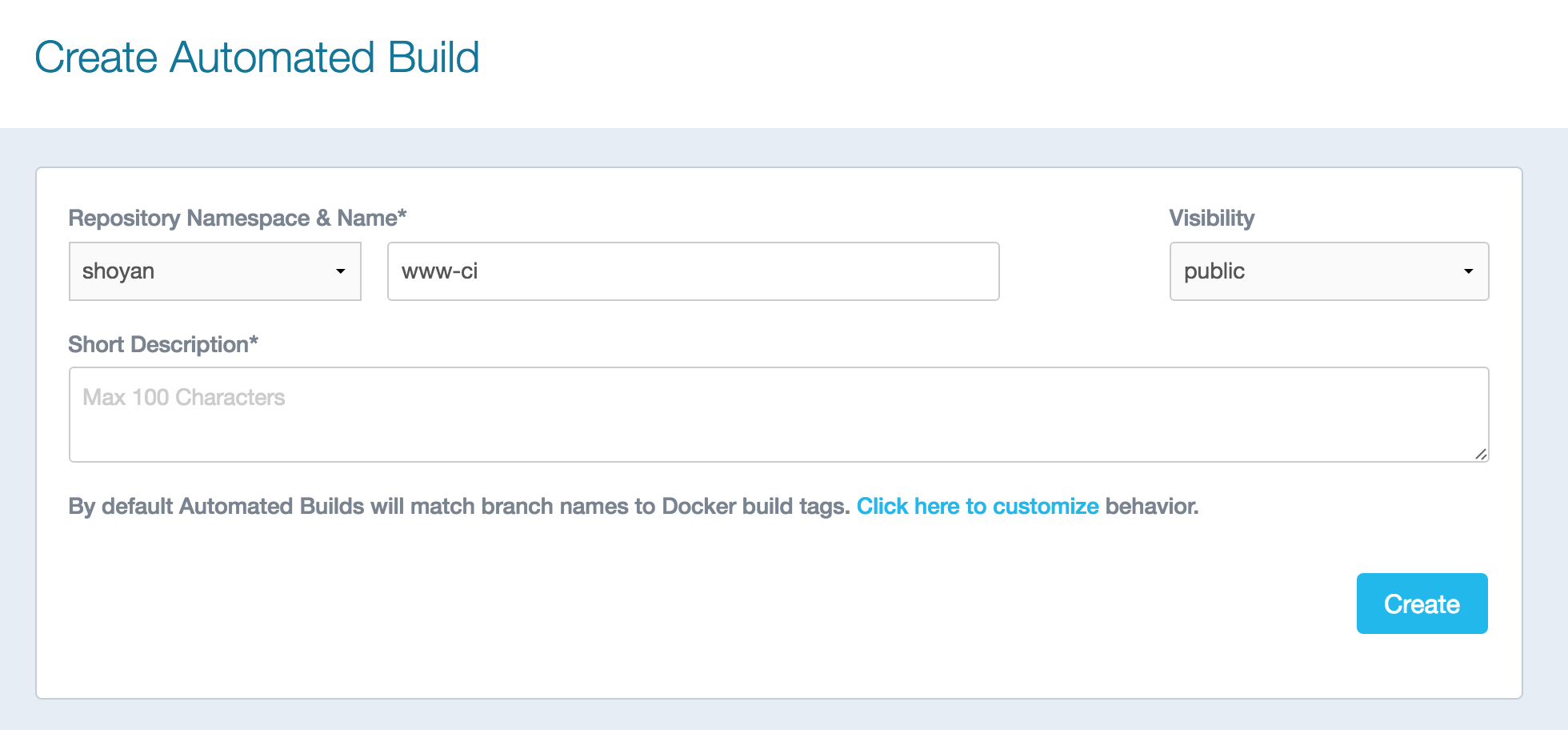
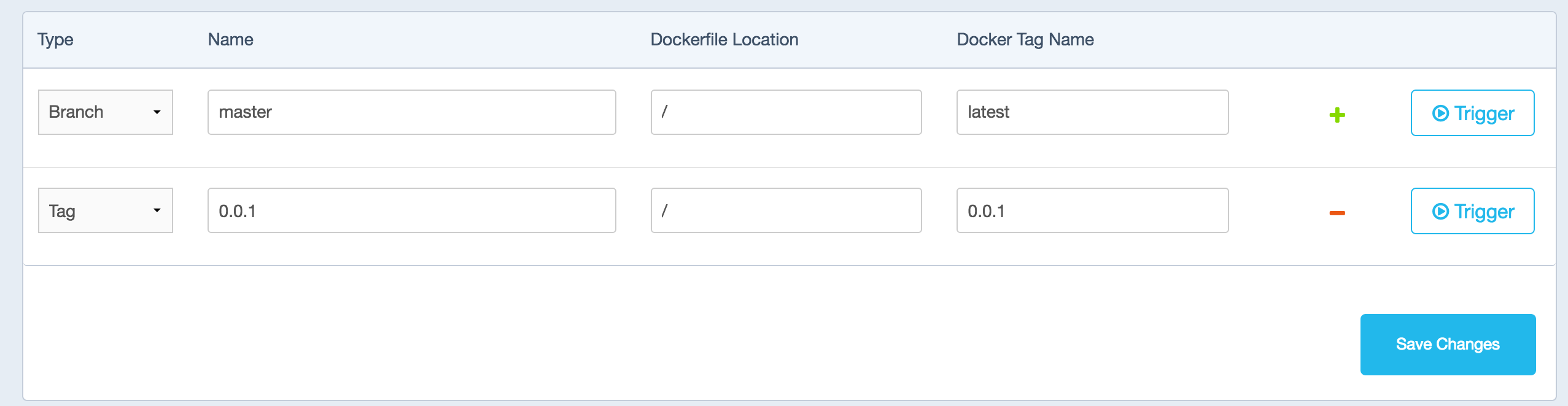
リポジトリの「Build Settings」でビルドの設定ができます。

Triggerボタンを押すとビルドが始まります。

ビルドの状態は「Build Details」で確認できます。

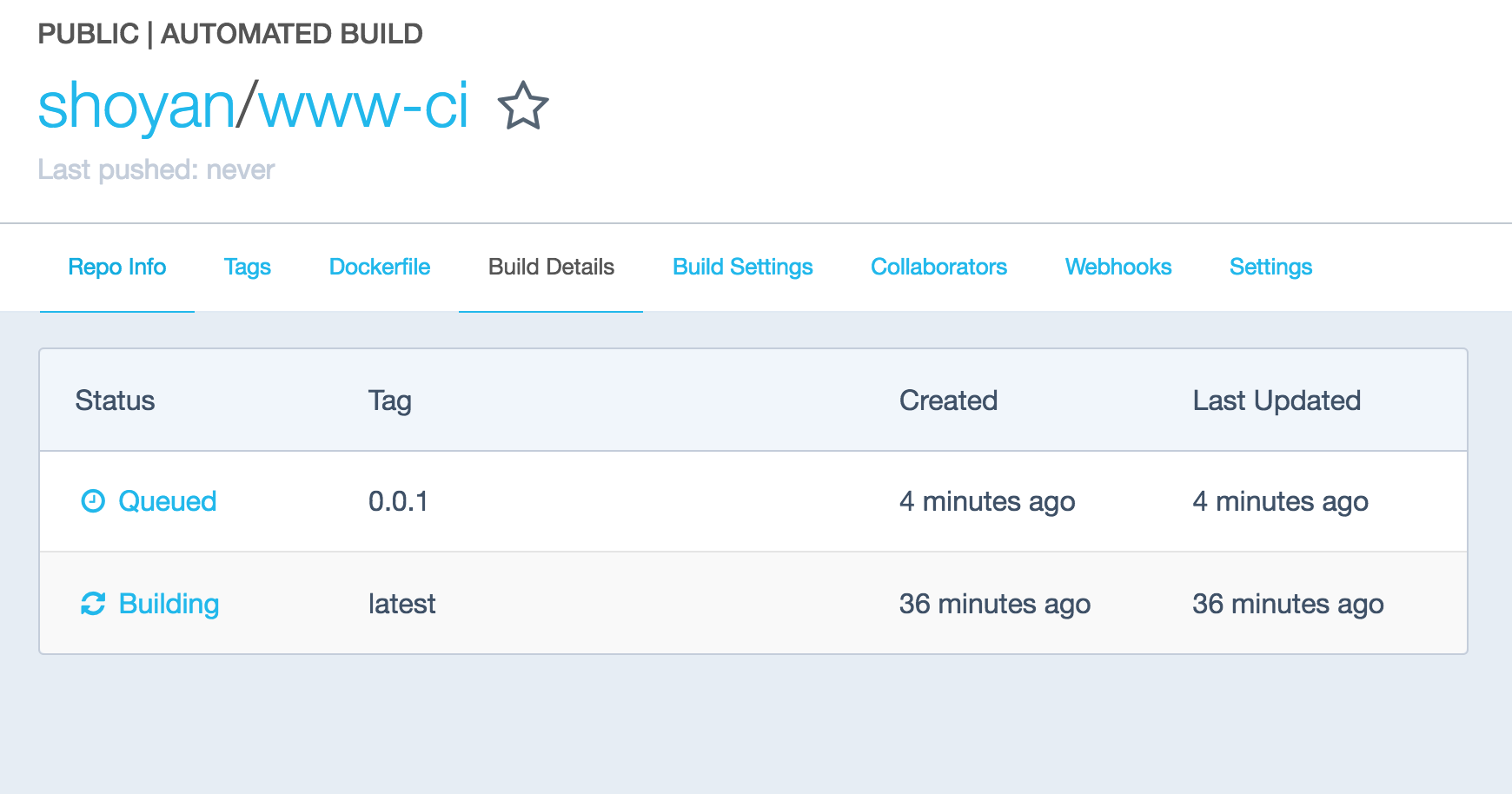
Queuedはビルド待ちのステータス。
Buildingはビルド中のステータスです。

GitHubにpushすればBuild Settingsで設定したブランチが自動的にビルドされます。

以上、簡単ですがDockerの自動ビルドの設定方法の紹介でした。
英語版ですが、詳しい方法が書いてあるのでこちらも参考にしてください。

• Automated Builds on Docker Hub

前回はRubotyのインストールとプラグインチュートリアルでRubotyの導入方法を紹介しました。
今回はRubotyをSlackで動かす方法を紹介します。

RubotyにはSlackアダプターが用意してありますが、新しくユーザーの作成が必要です。
ユーザーの作成が必要のない、Botsインテグレーションとruboty-slack_rtmを使ってRubotyをSlackで動かす方法を紹介します。

ruboty-slack_rtmのインストール

Gemfileに以下を定義します。

1

gem "ruboty-slack_rtm"

bundle install コマンドでインストールします。

SlackのBotsインテグレーションを設定する

Slackの管理画面でBotsインテグレーションを登録します。

登録するとTokenが発行されるので、そのTokenをSLACK_TOKENという名前で環境変数に設定します。
Rubotyは dotenv に対応しているので、.env ファイルを作成し、そこにTOKENを登録しておくと便利です。

.env

1

SLACK_TOKEN=<slack token>

Ruboty を起動します。.env ファイルを読み込むように —dotenv オプションをつけて起動します。

1

bundle exec ruby --dotenv

起動すると SlackのRubotyがログインマークに変わります。

あとは、チャンネルにinviteすればSlackでRubotyが使えます！
ちなみにrubotyではなく、Botsインテグレーションで登録したユーザー名に反応します。

関連記事

• Rubotyのインストールとプラグインチュートリアル